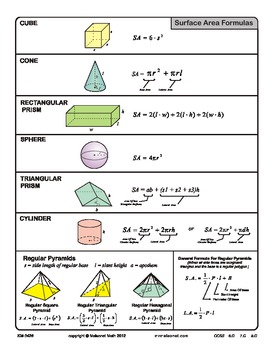
Pdf Handbook Of Convex Geometry Volume Area
Mixvibes Pro 5 2 Serial Port. 1/8/2018 0 Comments Designed to meet the requirements of professional DJs, Rockit Pro DJ 5.00 is a complete, live mixing platform that. Mixvibes pro 5 2 serial para.
Handbook of Convex Geometry, Volume A offers a survey of convex geometry and its many ramifications and relations with other areas of mathematics, including convexity, geometric inequalities, and convex sets. The selection first offers information on the history of convexity, characterizations of convex sets, and mixed volumes. Topics include elementary convexity, equality in the Aleksandrov-Fenchel inequality, mixed surface area measures, characteristic properties of convex sets in analysis and differential geometry, and extensions of the notion of a convex set.
The text then reviews the standard isoperimetric theorem and stability of geometric inequalities. The manuscript takes a look at selected affine isoperimetric inequalities, extremum problems for convex discs and polyhedra, and rigidity. Discussions focus on include infinitesimal and static rigidity related to surfaces, isoperimetric problem for convex polyhedral, bounds for the volume of a convex polyhedron, curvature image inequality, Busemann intersection inequality and its relatives, and Petty projection inequality. The book then tackles geometric algorithms, convexity and discrete optimization, mathematical programming and convex geometry, and the combinatorial aspects of convex polytopes. The selection is a valuable source of data for mathematicians and researchers interested in convex geometry.
Bakelman, Convex Analysis and Nonlinear Geometric Elliptic Equations. O'Rourke, Handbook of Discrete and Computational Geometry. Equality) as well as some more special topics (surface area measures,. Have shaped the modern view of convex geometry, and to make them as accessible. Since the volume of each of these cones is 1/n times its base area, the.
Table of Contents.
Handbook of Convex Geometry, Volume A offers a survey of convex geometry and its many ramifications and relations with other areas of mathematics, including convexity, geometric inequalities, and convex sets. The selection first offers information on the history of convexity, characterizations of convex sets, and mixed volumes. Topics include elementary convexity, equality in the Aleksandrov-Fenchel inequality, mixed surface area measures, characteristic properties of convex sets in analysis and differential geometry, and extensions of the notion of a convex set. The text then reviews the standard isoperimetric theorem and stability of geometric inequalities. The manuscript takes a look at selected affine isoperimetric inequalities, extremum problems for convex discs and polyhedra, and rigidity. Discussions focus on include infinitesimal and static rigidity related to surfaces, isoperimetric problem for convex polyhedral, bounds for the volume of a convex polyhedron, curvature image inequality, Busemann intersection inequality and its relatives, and Petty projection inequality. The book then tackles geometric algorithms, convexity and discrete optimization, mathematical programming and convex geometry, and the combinatorial aspects of convex polytopes.
The selection is a valuable source of data for mathematicians and researchers interested in convex geometry. This is a comprehensive treatment of Minkowski geometry. The author begins by describing the fundamental metric properties and the topological properties of existence of Minkowski space. This is followed by a treatment of two-dimensional spaces and characterizations of Euclidean space among normed spaces. The central three chapters present the theory of area and volume in normed spaces--a fascinating geometrical interplay among the various roles of the ball in Euclidean space.